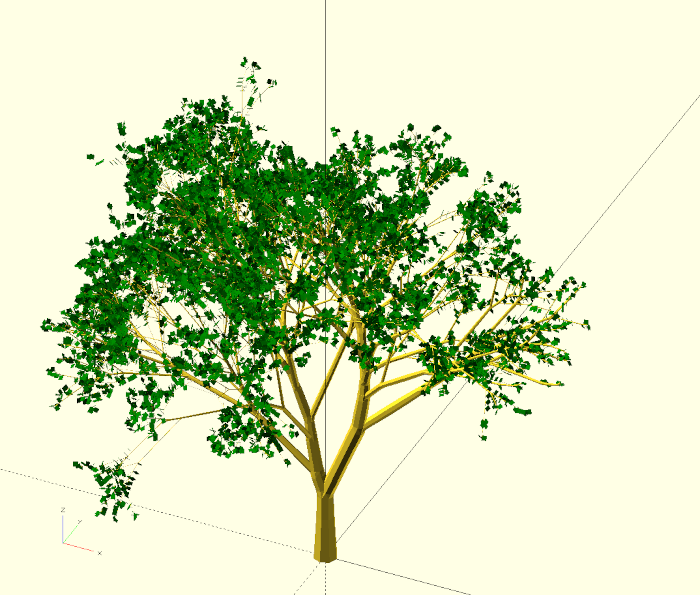
Natural structures, such as the shape of plants, often arise from growth processes that are based on relatively simple rules. By means of recursive geometry descriptions we can reproduce such growth processes in a simplified form and generate complex geometries that resemble these natural structures. In this project, we want to reproduce the appearance of a tree using such a recursive geometry description.

We have already seen that recursive functions can be used to define iterative algorithms in OpenSCAD. Here we will learn about the possibility to use recursion also in the geometry description itself. Furthermore, we will see how to generate random numbers using the rands function.
A warning must be given right at the beginning: recursive geometries can grow very quickly in their complexity and bring practically every computer system very quickly to its respective limits. Especially the so-called recursion depth, which is a parameter of every recursive geometry description, is crucial in this regard. In the following design, you should change this parameter only with extreme caution.
The basic idea for our recursive tree is to let the tree grow step by step as in a growth process. Each step will be recursive. Let’s start with a minimal geometry description:
module r_tree(
h_increment,
main_depth,
){
linear_extrude( height = h_increment )
children(0);
if (main_depth > 0) {
translate( [0, 0, h_increment] )
r_tree(
h_increment,
main_depth - 1
) {
children(0);
}
}
}
r_tree(
h_increment = 10,
main_depth = 20
) {
circle( d = 10, $fn=8);
}The module r_tree has two parameters h_increment and main_depth so far. The h_increment sets the height by which we want to grow each step. The main_depth specifies how many more steps we can go in the current section of the tree. Inside the module, we first create a piece of the tree using linear extrusion of the 2D geometry passed to the module. Then we check if we have any more growth steps left (if (main_depth > 0) ...). If so, we recursively use the module r_tree as a geometry that is shifted up by h_increment. This recursive usage basically copies the module description of the module r_tree to that location in the description again. This is a bit like the effect of looking into two opposing mirrors resulting in an endless sequence of copies.
To prevent that this sequence of copies in our module description becomes endless, the parameter main_depth is key. In the recursive definition of r_tree, we reduce main_depth by 1. This way, main_depth becomes slightly smaller with each step, until finally main_depth takes the value 0 and the copying stops. In addition, we forward the outer geometry passed to our module to the recursive copy by appending children(0).
Next, we want to create some random variations in our module description. We can do this by using the rands function:
module r_tree(
h_increment,
main_depth,
rnd_seed
){
rnd_values = rands( 0, 1, 10, rnd_seed );
linear_extrude( height = h_increment )
children(0);
if (main_depth > 0) {
translate( [0, 0, h_increment] )
r_tree(
h_increment,
main_depth - 1 - rnd_values[0] * 2,
rnd_values[9] * 100
) {
children(0);
}
}
}
r_tree(
h_increment = 10,
main_depth = 20,
rnd_seed = 42
) {
circle( d = 10, $fn=8);
}The function rands (short for random values) creates an array of random numbers. The first two parameters specify the lower and upper bound of these numbers. In our case we generate random decimal numbers between 0 and 1. The third parameter specifies how many random numbers the array should contain. We let rands generate 10 numbers for now, since we’ll be sprinkling in “randomness” at various points within our module. The last parameter is an initialization value that we define externally via the module parameter rnd_seed. The random numbers generated by the rands function are not really random. They only look like that. In reality, they are just pseudo-random numbers that have a fixed order. The initialization value (an arbitrary number), determines this order. This has the advantage that with different initialization values we get different sequences of random numbers, but at the same time we keep control over the random sequences. If we do not change the initialization value, we always get the same sequence of numbers. Specifically, for our tree, this means that we can change the rnd_seed parameter of our module to generate a new tree variant. If we like the variant, we can remember the value of rnd_seed and thus recreate the respective variant. If this would not be the case and the random numbers were truly random, we would get a different tree every time we computed the geometry.
In our module r_tree we use the random numbers in two places. First, we reduce the main_depth in the recursive definition of r_tree not only by one, but also by a random value between 0 and 2 (random[0] * 2). For this we use the first of our ten random numbers. Second, we pass the last of our ten random numbers to the recursive instance as a new rnd_seed value. We scale the value to a range between 0 and 100, since the documentation of rands is a bit unclear whether it requires integers or decimal values for initialization. By scaling the number we’re just playing it safe here. If you now change the value of rnd_seed in the test instance of the module r_tree and run a preview (F5), you will see how the height of our “tree” changes randomly with each value of rnd_seed.
The trunk and branches of trees are predominantly straight, but do show variations in their thickness and become thinner in the direction of growth. We can model this via a scaling parameter:
module r_tree(
h_increment,
main_depth,
rnd_seed,
scaling,
s_variance
){
rnd_values = rands( 0, 1, 10, rnd_seed );
function z(from, to, idx) = rnd_values[idx] * (to - from) + from;
sf = scaling + z(-1, 1 ,1) * s_variance;
linear_extrude( height = h_increment, scale = sf )
children(0);
if (main_depth > 0) {
translate( [0, 0, h_increment] )
r_tree(
h_increment,
main_depth - 1 - z(0,2,0),
z(0,100,9),
scaling,
s_variance
) {
scale( [sf, sf] )
children(0);
}
}
}
r_tree(
h_increment = 10,
main_depth = 20,
rnd_seed = 42,
scaling = 0.97,
s_variance = 0.1
) {
circle( d = 10, $fn=8);
}We have added two new parameters to our module r_tree. The parameter scaling specifies to what percentage the passed basic shape should shrink in each step. The parameter s_variance sets the random variation of the scaling. Inside the module, we first cleaned it up a bit and defined a function z that gives us a random value from the random array and scales it to an interval [from,to]. This makes further use of random numbers in our module a bit more convenient. Next, we determine a scaling factor sf from the parameters scaling and s_variance that is applied to the current step of the recursion. We pass sf to the linear extrusion (linear_extrude) as parameter scale. To ensure that the next tree section now neatly connects to the scaled basic shape, we have to scale it accordingly (scale( [sf, sf] )) when passing it to the recursive usage of r_tree.
Our tree is currently nothing more than a single branch. To change this, we need to fork (at least) one branch at some point during our simulated growth process. To prevent us from branching infinitely often, we need to introduce another recursion depth variable branch_depth for this new recursion path:
module r_tree(
h_increment,
md_init,
main_depth,
rnd_seed,
scaling,
s_variance,
bd_init,
branch_depth,
branch_angle
){
/* ... */
linear_extrude( height = h_increment, scale = sf )
children(0);
// should we branch?
if (
(branch_depth > 0) &&
(z(0, 0.8 ,2) < ((md_init - main_depth) / md_init) )
){
r_angle = z(0, 720, 3);
br_angle = branch_angle / 2 + z(0, 0.5, 4) * branch_angle;
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [br_angle, 0, 0] )
r_tree(
h_increment,
md_init,
main_depth,
z(0,100, 5),
scaling,
s_variance,
bd_init,
branch_depth - 1,
branch_angle
) {
scale( [sf, sf] )
children(0);
}
}
if (main_depth > 0) {
translate( [0, 0, h_increment] )
r_tree(
h_increment,
md_init,
main_depth - 1 - z(0,2,0),
z(0,100, 9),
scaling,
s_variance,
bd_init,
branch_depth,
branch_angle
) {
scale( [sf, sf] )
children(0);
}
}
}
r_tree(
h_increment = 10,
md_init = 20,
main_depth = 20,
rnd_seed = 42,
scaling = 0.97,
s_variance = 0.1,
bd_init = 1,
branch_depth = 1,
branch_angle = 30
) {
circle( d = 10, $fn=8);
}We have extended our module r_tree by some parameters. The two init parameters md_init and bd_init contain the initial values of the parameters main_depth and branch_depth. We need these initial values to be able to start “fresh” with a new branch in case of a fork. In addition, we have introduced the parameter branch_angle, with which we define the (maximum) angle of the branching process.
After the geometry description of our current branch section (linear_extrude ...), we decide whether a new branch should break off at this point. We do this only if two conditions are met: the branch_depth must be greater than 0 (safe recursion end!) and (&&) a random value between 0 and 0.8 must be smaller than a certain ratio between the current main depth and the initial main depth ((md_init - main_depth) / md_init). Why is that? Let’s put in some numbers to see how the ratio changes over time. At the beginning, the current main_depth is equal to the initial main depth md_init. This makes the ratio 0. That a random value from the interval 0 to 0.8 is smaller than 0 is impossible. At the end, the current main_depth is 0. Then the ratio becomes 1. In this case, it is guaranteed that a random value from the interval 0 to 0.8 is smaller. In other words, the further our branch grows, the more likely it is that a new branch will be forked.
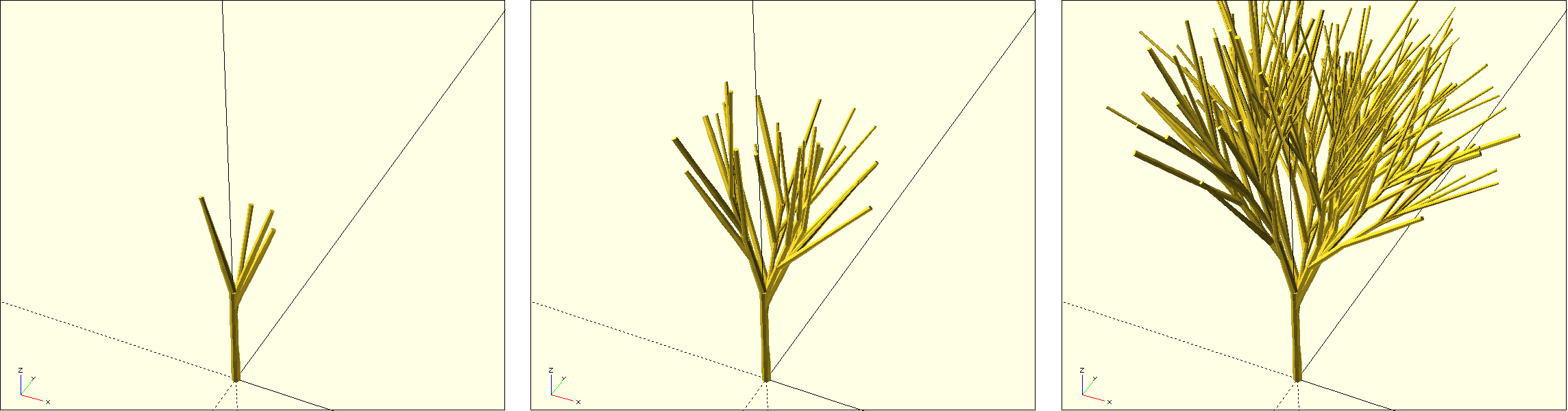
Inside the if-statement we first define two angles r_angle and br_angle. The rotation angle r_angle is a random angle that determines in which direction the branch should branch off. The branch angle br_angle determines the concrete branch angle of the branch as a mixture of the parameter branch_angle and a random part. Subsequently, the new branch is described by recursively using the module r_tree, which is now rotated before being shifted by h_increment. The main_depth of this new branch is reset to md_init. The branch_depth, on the other hand, is decreased by 1. Figure 10. shows the effect of this second recursion path for recursion depths of 1, 2, and 3.
Our branches seem a bit unrealistically long at the moment, and they do kind of pile up unnaturally depending on chance. Let’s address the first problem by assuming that the height increment should decrease as the recursion depth increases. We can make this possible via another parameter r_decrement for the increment reduction:
module r_tree(
h_increment,
r_decrement,
md_init,
main_depth,
rnd_seed,
scaling,
s_variance,
bd_init,
branch_depth,
branch_angle
){
/* ... */
// should we branch?
if (
(branch_depth > 0) &&
(z(0, 0.8 ,2) < ((md_init - main_depth) / md_init) )
){
r_angle = z(0, 720, 3);
br_angle = branch_angle / 2 + z(0, 0.5, 4) * branch_angle;
new_increment =
h_increment -
h_increment / 2.5 * pow(r_decrement, branch_depth);
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [br_angle, 0, 0] )
r_tree(
new_increment,
r_decrement,
md_init,
md_init,
z(0,100, 5),
scaling,
s_variance,
bd_init,
branch_depth - 1,
branch_angle
) {
scale( [sf, sf] )
children(0);
}
}
if (main_depth > 0) {
translate( [0, 0, h_increment] )
r_tree(
h_increment,
r_decrement,
md_init,
main_depth - 1 - z(0,2,0),
z(0,100,9),
scaling,
s_variance,
bd_init,
branch_depth,
branch_angle
) {
scale( [sf, sf] )
children(0);
}
}
}
r_tree(
h_increment = 10,
r_decrement = 0.7,
/* ... */
) {
circle( d = 10, $fn=8);
}We use a power function for the decrease of the height increment. Since r_decrement is less than 1, higher powers make the resulting value smaller. In other words: with increasing recursion depth the reduction of the height increment increases.
Make sure that you update the parameter lists at all occurences of the module r_tree. Unfortunately, due to a bug in OpenSCAD, we cannot set default values for the parameters and have to specify them completely each time. If you try to use default parameters, OpenSCAD crashes with a memory error after a certain number of parameters.
Now we can take care of the second problem. The forked branches start with the same size as the branch from which they emerge. This is not very realistic. The size of the forked branch should be smaller and also depend on its angle. If the angle is large, the diameter should be rather small. In addition, the main branch should also lose some of its diameter and, depending on the angle of the forked branch, should give way to it somewhat. Let us convert these thoughts into a geometry description:
module r_tree(
h_increment,
r_decrement,
md_init,
main_depth,
rnd_seed,
scaling,
s_variance,
bd_init,
branch_depth,
branch_angle,
branch_min_size,
branch_max_size
){
/* ... */
// should we branch?
if (
(branch_depth > 0) &&
(z(0, 0.8 ,2) < ((md_init - main_depth) / md_init) )
){
/* ... */
// goes to 0, if br_angle is large
// goes to 1, if br_angle is small
branch_ratio = (branch_angle / br_angle) - 1.0;
branch_scaling =
branch_min_size * branch_ratio +
branch_max_size * (1.0 - branch_ratio);
main_scaling =
sf * branch_ratio +
branch_max_size * (1.0 - branch_ratio);
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [br_angle, 0, 0] )
r_tree(
new_increment,
r_decrement,
md_init,
md_init,
z(0,100, 5),
scaling,
s_variance,
bd_init,
branch_depth - 1,
branch_angle,
branch_min_size,
branch_max_size
) {
scale( [branch_scaling, branch_scaling] )
children(0);
}
// main path rotated in counter-direction
if (main_depth > 0) {
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [-(branch_angle - br_angle), 0, 0] )
r_tree(
new_increment,
r_decrement,
md_init,
main_depth - 1 - z(0,2, 6),
z(0,100, 7),
scaling,
s_variance,
bd_init,
branch_depth,
branch_angle,
branch_min_size,
branch_max_size
) {
scale( [main_scaling, main_scaling] )
children(0);
}
}
} else {
if (main_depth > 0) {
translate( [0, 0, h_increment] )
r_tree(
h_increment,
r_decrement,
md_init,
main_depth - 1 - z(0,2,0),
z(0,100,9),
scaling,
s_variance,
bd_init,
branch_depth,
branch_angle,
branch_min_size,
branch_max_size
) {
scale( [sf, sf] )
children(0);
}
}
}
}
r_tree(
/* ... */
branch_min_size = 0.3,
branch_max_size = 0.8
) {
circle( d = 10, $fn=8);
}The geometry description has become a lot more extensive! We have added two new parameters branch_min_size and branch_max_size. These determine the size range of forked branches in relation to the size of the main branch. Inside the module, we have moved the case where we do not branch into an else block. This means that in the case of branching, we do not continue growing straight ahead with the main branch but stop the normal growth.
Within the description of the branch, we first determine a branch_ratio and use this to define new scaling factors for both the forked branch and the main branch (branch_scaling and main_scaling). In the subsequent definition of the forked branch, branch_scaling is then used to scale the forwarded children(0) geometry. After the definition of the forked branch follows a new definition of the main branch. Here, too, it is first checked whether the main branch should be continued at all (if (main_depth > 0)). In contrast to the normal main branch growth, the main branch is now rotated away from the forked branch (rotate( [-(branch_angle - br_angle), 0, 0] )) and the geometry of the continued main branch is scaled by main_scaling. In addition, the main branch now also adopts the new_increment value of the forked branch. If you set bd_init and branch_depth to 3 or even 4 as a test, you can see that we are on the right track.

If you look closely, you can see that the junctions at the branch points still look very rough (Figure 10.). We can solve this with the help of hull transformations:
module r_tree(
/* ... */
){
/* ... */
// should we branch?
if (
(branch_depth > 0) &&
(z(0, 0.8 ,2) < ((md_init - main_depth) / md_init) )
){
/* ... */
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [br_angle, 0, 0] )
r_tree(
/* ... */
) {
scale( [branch_scaling, branch_scaling] )
children(0);
}
// smooth out connection to branching path
hull() {
translate( [0, 0, h_increment] )
linear_extrude( height = 0.01 )
scale([sf,sf])
children(0);
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [br_angle, 0, 0] )
linear_extrude(
height = new_increment / 2,
scale = pow(scaling,1/3)
)
scale( [branch_scaling, branch_scaling] )
children(0);
}
// main path rotated in counter-direction
if (main_depth > 0) {
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [-(branch_angle - br_angle), 0, 0] )
r_tree(
/* ... */
) {
scale( [main_scaling, main_scaling] )
children(0);
}
// smooth out connection to main path
hull() {
translate( [0, 0, h_increment] )
linear_extrude( height = 0.01 )
scale([sf,sf])
children(0);
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [-(branch_angle - br_angle), 0, 0] )
linear_extrude(
height = new_increment / 2,
scale = pow(scaling,1/3)
)
scale( [main_scaling, main_scaling] )
children(0);
}
}
} else {
if (main_depth > 0) {
translate( [0, 0, h_increment] )
r_tree(
h_increment,
r_decrement,
md_init,
main_depth - 1 - z(0,2,0),
z(0,100,9),
scaling,
s_variance,
bd_init,
branch_depth,
branch_angle,
branch_min_size,
branch_max_size
) {
scale( [sf, sf] )
children(0);
}
}
}
}
r_tree(
h_increment = 10,
r_decrement = 0.7,
md_init = 20,
main_depth = 20,
rnd_seed = 42,
scaling = 0.97,
s_variance = 0.1,
bd_init = 1,
branch_depth = 1,
branch_angle = 30,
branch_min_size = 0.3,
branch_max_size = 0.8
) {
circle( d = 10, $fn=8);
}For smoothing the junctions we instantiate the outer geometry (children(0)) twice. We position one instance at the end of the current growth section and the other instance at the beginning of the branch or at the beginning of the rotated main branch. We give the latter instance half the height of the next growth section and scale it accordingly. Then we use the hull transformation to connect both “tree slices” and thus bridge the existing gaps (Figure {{imginc>}}{}).

What we are still missing are the leaves of the tree. We can use the branch depth to draw leaves instead of a branch in the last recursion step:
module r_tree(
/* ... */
){
rnd_values = rands( 0, 1, 10, rnd_seed );
function z(from, to, idx) = rnd_values[idx] * (to - from) + from;
if ((branch_depth < 1) && ($children > 1)) {
color("green")
rotate([(floor(rnd_seed) % 2 == 0) ? 45 : -45,0,0])
linear_extrude(height = 0.1)
children(1);
} else {
/* ... */
// should we branch?
if (
(branch_depth > 0) &&
(z(0, 0.8 ,2) < ((md_init - main_depth) / md_init) )
){
/* ... */
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [br_angle, 0, 0] )
r_tree(
/* ... */
) {
scale( [branch_scaling, branch_scaling] )
children(0);
if ($children > 1) children(1);
}
// smooth out connection to branching path
/* ... */
// main path rotated in counter-direction
if (main_depth > 0) {
translate( [0, 0, h_increment] )
rotate( [0, 0, r_angle] )
rotate( [-(branch_angle - br_angle), 0, 0] )
r_tree(
/* ... */
) {
scale( [main_scaling, main_scaling] )
children(0);
if ($children > 1) children(1);
}
// smooth out connection to main path
/* ... */
}
} else {
if (main_depth > 0) {
translate( [0, 0, h_increment] )
r_tree(
/* ... */
) {
scale( [sf, sf] )
children(0);
if ($children > 1) children(1);
}
}
if ((branch_depth < 2) && ($children > 1)) {
color("green")
rotate([(floor(rnd_seed) % 2 == 0) ? 45 : -45,0,0])
linear_extrude(height = 0.1)
children(1);
}
}
}
}
r_tree(
/* ... */
bd_init = 4,
branch_depth = 4,
/* ... */
) {
circle( d = 10, $fn=8);
square([2,2]);
}As leaves we use the other geometry passed to our module from outside (here: square([2,2]);). Accordingly, we need to update all recursive uses of r_tree within our module and also pass the geometry children(1) along. However, we should only do this if a second geometry was actually passed. Therefore, we check $children everytime before we forward children(1). Since the yield of leaves is somewhat low if one draws the leaves only at the end of the recursion (if (branch_depth < 1)) we have defined the leaf geometry once more below the regular growth path and define it there when we are at the second to last recursion level (if (branch_depth < 2)). As we now only get a nice leaf canopy from a total recursion depth of about 4, we also adjusted the parameters of the test instance of our module r_tree. The expression (floor(rnd_seed) % 2 == 0) ? 45 : -45 causes the leaves to be rotated sometimes in one direction and sometimes in the other depending on whether the rounded down (floor) value of rnd_seed is even or odd. We have taken the value rnd_seed at this point, because it changes constantly. We could just as well have taken any other value from the random array.
With this we are done with our geometry description. If you want to automatically create some random trees, you can parameterize the test instance as follows:
srnd = rands(0,1000,1)[0];
echo(srnd);
r_tree(
h_increment = 10,
r_decrement = 0.7,
md_init = 20,
main_depth = 20,
rnd_seed = srnd,
scaling = 0.97,
s_variance = 0.1,
bd_init = 4,
branch_depth = 4,
branch_angle = 50,
branch_min_size = 0.3,
branch_max_size = 0.8
) {
circle( d = 10, $fn=8);
square([2,2]);
}The variable srnd now contains a single random number, which we use for the parameter rnd_seed of the module r_tree. Since we use the rands function without init parameter here, we get a new random number with each preview or render (F5 or F6). The echo command outputs the number to the OpenSCAD console. This way we can spot “good” init values that have produced nice trees. It is also worth varying the branch_angle parameter. The same applies to bd_init and branch_depth if your patience and the available processing power of your computer allow it. Figures 10. and 10.6 show two trees with 40 and 60 degrees branch angles respectively.